Решение определённых интегралов
Быстрый ответ
Примеры
Приведение к табличному виду
$$\int\limits_{0}^{1} \left(2^{x} + \frac{3 \sqrt[3]{5 x + 4}}{2}\right)\, dx$$
Метод непосредственного интегрирования
$$\int\limits_{0}^{1} 2^{3 x - 1}\, dx$$
Внесение под знак дифференциала/ Подведение под знак дифференциала
$$\int\limits_{0}^{1} \cos{2x}\, dx$$
$$\int\limits_{0}^{1} \ctg{x}\, dx$$
Интегрирование по частям
$$\int\limits_{0}^{1} x\cos{x}\, dx$$
$$\int\limits_{0}^{1} \arctg{2x}\, dx$$
Интегрирование методом подстановки
$$\int\limits_{0}^{1} \frac{1}{x*\sqrt{2x-9}}\, dx$$
Интегрирование заменой переменной
$$\int\limits_{0}^{1} \frac{1}{3-5x}\, dx$$
Интегрирование сложной функции
$$\int\limits_{0}^{1} x\exponentialE^{-x}\sin{-2\exponentialE^{-2x}}\, dx$$
Что такое определённый интеграл?
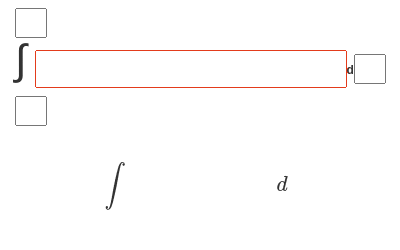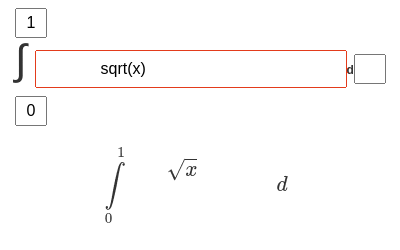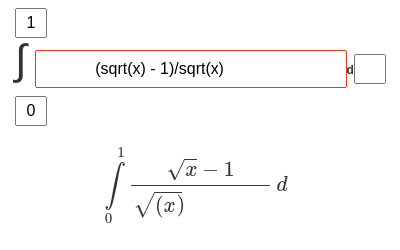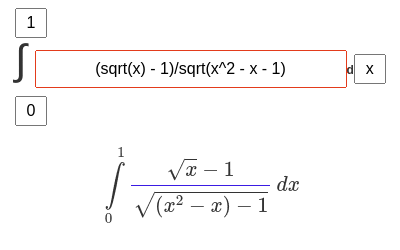
Что умеет?
Калькулятор предоставляет ПОДРОБНОЕ решение определённых интегралов
Этот калькулятор находит решение определенного интеграла от функции f(x) с данными верхними и нижними пределами
Что это вообще такое?
Подробнее про определённый интеграл вы можете посмотреть по ссылке
Решает различными методами и способами
Использует приведение к табличным интегралам
Метод непосредственного интегрирования (обратное от производной, найти первообразную)
Метод внесения под знак дифференциала/ Подведение под знак дифференциала
Используя формулу интегрирования по частям
Замена переменной в интеграле
Формула для сложной функции и метод замены