Исследование графика функции
Учитель очень удивится увидев твоё верное решение😉
Введите график функции
Исследуем график функции y=f(x), для этого задайте функцию f(x).
Калькулятор работает, доволен как слон
Примеры исследуемых функций
Исследование с помощью производной
y = x*sqrt(1 - x^2)
x^3 - 2*x^2 + 3
x^2 + cos(x)
y(x) = 3*x^2 - 2*x - 2
Наклонные асимптоты графика функции
(x^2 + x - 2)/x
e^(x/2)*(x + y^2)
2*sin(x) - 36/pi*x + 9
5*x^2*x^(1/3) - 3*sin(2*x)
Построение графика кусочно-непрерывной функции
$$\begin{cases} x + 2 & \text{for}\: x \geq -3 \wedge x < 0 \\2 - x & \text{for}\: x \geq 0 \wedge x \leq 4 \\0 & \text{otherwise} \end{cases}$$
1/x
y = x^4 - 6*x^2 + 4
Примеры
С применением степени
(квадрат и куб) и дроби
(x^2 - 1)/(x^3 + 1)
Квадратный корень
sqrt(x)/(x + 1)
Кубический корень
cbrt(x)/(3*x + 2)
С применением синуса и косинуса
2*sin(x)*cos(x)
Арксинус
x*arcsin(x)
Арккосинус
x*arccos(x)
Применение логарифма
x*log(x, 10)
Натуральный логарифм
ln(x)/x
Экспонента
exp(x)*x
Тангенс
tg(x)*sin(x)
Котангенс
ctg(x)*cos(x)
Иррациональные дроби
(sqrt(x) - 1)/sqrt(x^2 - x - 1)
Арктангенс
x*arctg(x)
Арккотангенс
x*arсctg(x)
Гиберболические синус и косинус
2*sh(x)*ch(x)
Гиберболические тангенс и котангенс
ctgh(x)/tgh(x)
Гиберболические арксинус и арккосинус
x^2*arcsinh(x)*arccosh(x)
Гиберболические арктангенс и арккотангенс
x^2*arctgh(x)*arcctgh(x)
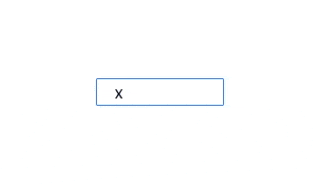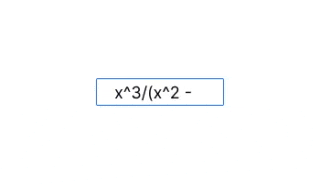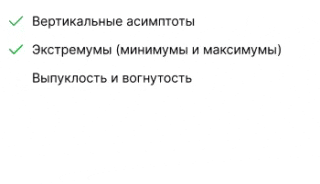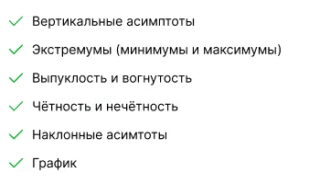
Что исследует?
Для периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
-
Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции: Да
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
- Минимум и максимум функции: Да
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
-
Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция - арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция - арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция - экспонента от x (что и e^x)
- log(x) or ln(x)
-
Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция - Синус от x
- cos(x)
- Функция - Косинус от x
- sinh(x)
- Функция - Синус гиперболический от x
- cosh(x)
- Функция - Косинус гиперболический от x
- sqrt(x)
- Функция - квадратный корень из x
- sqr(x) или x^2
- Функция - Квадрат x
- ctg(x)
- Функция - Котангенс от x
- arcctg(x)
- Функция - Арккотангенс от x
- arcctgh(x)
- Функция - Гиперболический арккотангенс от x
- tg(x)
- Функция - Тангенс от x
- tgh(x)
- Функция - Тангенс гиперболический от x
- cbrt(x)
- Функция - кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
- DiracDelta(x)
- Дельта-функция Дирака
- Heaviside(x)
- Функция Хевисайда
В выражениях можно применять следующие операции:
Другие функции:
Постоянные:
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- - умножение
- 3/x
- - деление
- x^3
- - возведение в степень
- x + 7
- - сложение
- x - 6
- - вычитание
- 15/7
- - дробь
Другие функции:
- asec(x)
- Функция - арксеканс от x
- acsc(x)
- Функция - арккосеканс от x
- sec(x)
- Функция - секанс от x
- csc(x)
- Функция - косеканс от x
- floor(x)
- Функция - округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция - округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция - Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция - гиперболический арксеканс от x
- csch(x)
- Функция - гиперболический косеканс от x
- sech(x)
- Функция - гиперболический секанс от x
- acsch(x)
- Функция - гиперболический арккосеканс от x
Постоянные:
- pi
- Число "Пи", которое примерно равно ~3.14159..
- e
- Число e - основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности - знак для бесконечности