Исследование графика функции

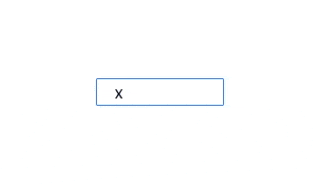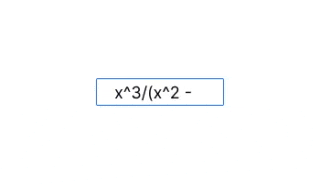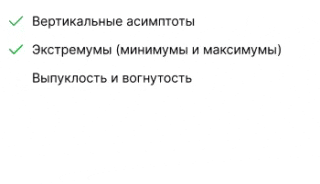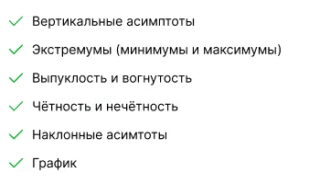
Примеры

x \sqrt{1 - x^{2}}

- \frac{36 x}{π} + 2 sin (x) + 9

x^{3} - 2 x^{2} + 3

5 x^{\frac{7}{3}} - 3 sin (2 x)

x^{2} + cos (x)

{\begin{cases} x + 2 & for x \geq - 3 \land x < 0 \\ 2 - x & for x \geq 0 \land x \leq 4 \\ 0 & в других случаях \end{cases}

y (x) = 3 x^{2} - 2 x - 2

\frac{1}{x}

\frac{x^{2} + x - 2}{x}

y = x^{4} - 6 x^{2} + 4

(x^{2} + x) e^{\frac{x}{2}}

y - (3 x^{2} - 1) = 0, y - (- \frac{3}{x}) = 0

atan (\frac{y}{x}) = x y

Область определения функции. Умеет определять точки, в которых знаменатель функции обращается в нуль

Умеет определять точки пересечения графика функции с осями координат

Экстремумы функции: интервалы (отрезки) возрастания и убывания функции

Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости)

Вертикальные асимптоты. (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)

Горизонтальные асимптоты графика функции

Наклонные асимптоты графика функции

Четность и нечетность функции

Минимум и максимум функции

Находит область значений функции

Детектирует стационарные точки

Выделяет период функции, если функция периодична