Вычисление криволинейных интегралов
Выберите тип криволинейного ∮ интеграла
I рода на плоскости
$$\int\limits_{\mathbf{L}} f{\left(x,y \right)} \,ds$$
II рода на плоскости
$$\int\limits_{\mathbf{L}} P{\left(x,y \right)} \,dx + Q{\left(x,y \right)} \,dy$$
I рода в пространстве
$$\int\limits_{\mathbf{L}} f{\left(x,y,z \right)} \,ds$$
II рода в пространстве
$$\int\limits_{\mathbf{L}} P{\left(M \right)} \,dx + Q{\left(M \right)} \,dy + R{\left(M \right)} \,dz $$
По замкнутому контуру
$$\oint\limits_{\mathbf{C}} P{\left(x,y \right)} \,dx + Q{\left(x,y \right)} \,dy $$
Примеры
Что умеет калькулятор криволинейных интегралов?
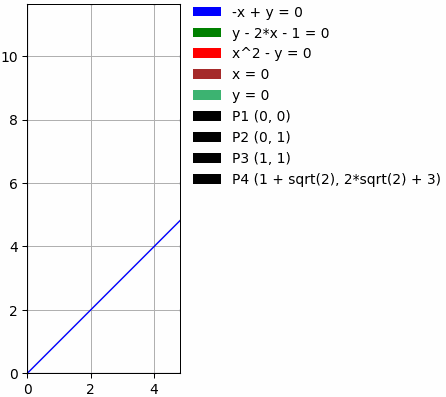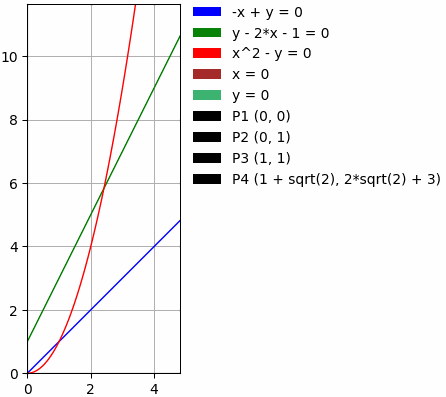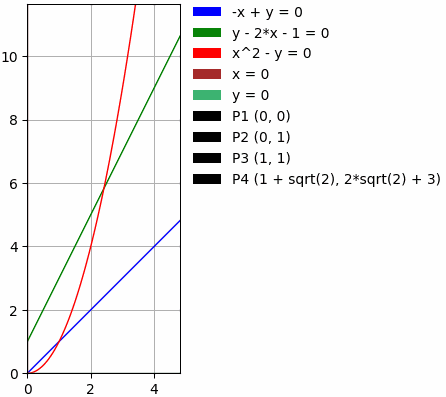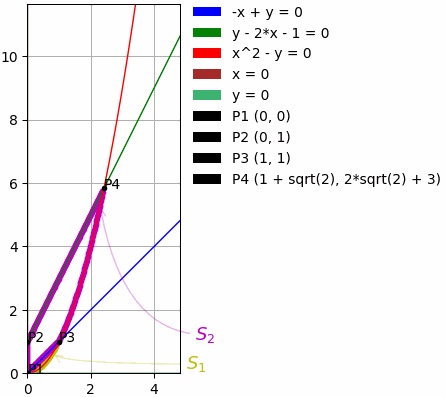
Что умеет?
Вычисляет криволинейный интеграл в направлении вдоль кривой
Вычисляет с помощью криволинейного интеграла длину кривой
Возможны случаи в декартовых и полярных координатах, а также заданных параметрически
Случаи незамкнутой кривой или криволинейного интеграла по замкнутому контуру
Вычисляет массу дуги кривой с заданной плотностью
Поддерживаемые типы
1-го рода
2-го рода
по замкнутому контуру