Пример использования сервиса по нахождению определителя матрицы

1. Попробуем сначала матрицу с обычными неизвестными  a, b и q и числами:
Введём здесь матрицу, как изображено на рис. ниже 
Форма онлайн ввода определителя матрицы
После того, как вы нажмёте кнопку "Далее", вы получите следующее подробное решение:

 

Дана матрица А= 
[q  0  -q]
[        ]
[3  4  -b]
[        ]
[a  q  0 ]

Вычисляем последовательно детерминант det(A):

[q  0  -q]
[        ]
[3  4  -b]
[        ]
[a  q  0 ]
 = + (q) *( 
[4  -b]
[     ]
[q  0 ]
 ) - (0) *( 
[3  -b]
[     ]
[a  0 ]
 ) + (-q) *( 
[3  4]
[    ]
[a  q]
 ) 
[4  -b]
[     ]
[q  0 ]
 = + (4) *( 
[0]
 ) - (-b) *( 
[q]
 ) 
[3  -b]
[     ]
[a  0 ]
 = + (3) *( 
[0]
 ) - (-b) *( 
[a]
 ) 
[3  4]
[    ]
[a  q]
 = + (3) *( 
[q]
 ) - (4) *( 
[a]
 )

Значит, после выполнения простейших арифметических операций (сложение и умножения чисел) в последних детерминантах, и подстановке их значений в детерминанты выше,

получаем det(A) = det( 
[q  0  -q]
[        ]
[3  4  -b]
[        ]
[a  q  0 ]
 ) =
4*a*q + b*q^2 - 3*q^2
 
2. Второй пример с использованием функций синус и косинус: sin(x) и cos(x):
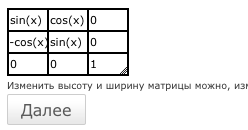
sin и cos в детерминанте онлайн
Нажмёте кнопку "Далее", получите ответ:

 

Дана матрица А= 
[sin(x)   cos(x)  0]
[                  ]
[-cos(x)  sin(x)  0]
[                  ]
[   0       0     1]

Вычисляем последовательно детерминант det(A):

[sin(x)   cos(x)  0]
[                  ]
[-cos(x)  sin(x)  0]
[                  ]
[   0       0     1]
 = + (sin(x)) *( 
[sin(x)  0]
[         ]
[  0     1]
 ) - (cos(x)) *( 
[-cos(x)  0]
[          ]
[   0     1]
 ) + (0) *( 
[-cos(x)  sin(x)]
[               ]
[   0       0   ]
 ) 
[sin(x)  0]
[         ]
[  0     1]
 = + (sin(x)) *( 
[1]
 ) - (0) *( 
[0]
 ) 
[-cos(x)  0]
[          ]
[   0     1]
 = + (-cos(x)) *( 
[1]
 ) - (0) *( 
[0]
 ) 
[-cos(x)  sin(x)]
[               ]
[   0       0   ]
 = + (-cos(x)) *( 
[0]
 ) - (sin(x)) *( 
[0]
 )

Значит, после выполнения простейших арифметических операций (сложение и умножения чисел) в последних детерминантах, и подстановке их значений в детерминанты выше,

получаем det(A) = det( 
[sin(x)   cos(x)  0]
[                  ]
[-cos(x)  sin(x)  0]
[                  ]
[   0       0     1]
 ) = = sin(x)^2 + cos(x)^2

3. Ещё один пример - с простыми и отрицательными числами и определителем квадратной матрицей 2x2 (предыдущие примеры были с матрицей 3x3):

Сначала изменим размер матрицы до 2 на 2, после введём заданные числа, так, как на рис. ниже:

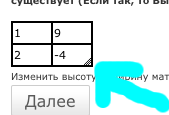
Определитель матрицы 2 на 2

Результат решения детерминанта матрицы 2 на 2:

Дана матрица А= 
[1  9 ]
[     ]
[2  -4]

Вычисляем последовательно детерминант det(A):

[1  9 ]
[     ]
[2  -4]
 = + (1) *( 
[-4]
 ) - (9) *( 
[2]
 )

Значит, после выполнения простейших арифметических операций (сложение и умножения чисел) в последних детерминантах, и подстановке их значений в детерминанты выше,

получаем det(A) = det( 
[1  9 ]
[     ]
[2  -4]
 ) = = -22