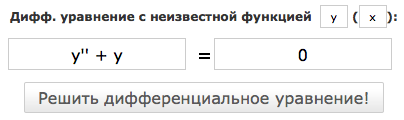
Рассмотрим примеры того, как решить однородные и неоднородные линейные дифференциальные уравнения с постоянными коэффициентами с помощью калькулятора дифференциальных уравнений.
Для того чтобы решить линейное дифф. ур-ние с постоянными коэф. онлайн, зайдите на страницу калькулятора:
Рассмотрим сначала пример с однородным уравненим:
2
d d
3*--(y(x)) + ---(y(x)) = 0
dx 2
dx
Для этого в форму нужно ввести вот такое выражение:
3*y' + y'' = 0
Вы получите такое подробное решение:
Дано уравнение:
::
2
d d
3*--(y(x)) + ---(y(x)) = 0
dx 2
dx
Это дифф. уравнение имеет вид:
::
y'' + p*y' + q*y = 0,
где
::
p = 3
::
q = 0
Называется линейным однородным
дифф. ур-нием 2-го порядка с постоянными коэффициентами.
Решить это ур-ние не представляет особой сложности
Сначала отыскиваем корни характеристического ур-ния
::
2
k + p*k + q = 0
В нашем случае характ. ур-ние будет иметь вид:
::
2
k + 3*k = 0
- это простое квадратное ур-ние
Корни этого ур-ния:
::
k1 = -3
::
k2 = 0
Т.к. характ. ур-ние имеет два корня,
и корни не имеют комплексный вид, то
решение соотв. дифф. ур-ния имеет вид:
::
k1*x k2*x
y(x) = C1*e + C2*e
Получаем окончательный ответ:
::
-3*x
y(x) = C2 + C1*e
Далее, рассмотрим пример с неоднородным дифференциальным уравнением:
2
d d / 2\ x
- 2*--(y(x)) + ---(y(x)) = \1 + x /*e
dx 2
dx
Указанный пример можно ввести в форму калькулятора так:
-2*y' + y'' = (1 + x^2)*exp(x)
После Вы получите подробный ответ:
Дано уравнение:
::
2
d d / 2\ x
- 2*--(y(x)) + ---(y(x)) = \1 + x /*e
dx 2
dx
Это дифф. уравнение имеет вид:
::
y'' + p*y' + q*y = s,
где
::
p = -2
::
q = 0
::
/ 2\ x
s = -\1 + x /*e
Называется линейным однородным
дифф. ур-нием 2-го порядка с постоянными коэффициентами.
Решить это ур-ние не представляет особой сложности
Сначала отыскиваем корни характеристического ур-ния
::
2
k + p*k + q = 0
В нашем случае характ. ур-ние будет иметь вид:
::
2
k - 2*k = 0
- это простое квадратное ур-ние
Корни этого ур-ния:
::
k1 = 0
::
k2 = 2
Т.к. характ. ур-ние имеет два корня,
и корни не имеют комплексный вид, то
решение соотв. дифф. ур-ния имеет вид:
::
k1*x k2*x
y(x) = C1*e + C2*e
::
2*x
y(x) = C1 + C2*e
Мы нашли решение соотв. однородного ур-ния
Теперь надо решить наше неоднородное уравнение
::
y'' + p*y' + q*y = s
Используем метод вариации произвольной постоянной
Считаем, что C1 и C2 - это функции от x
И общим решением будет:
::
2*x
y(x) = C2(x)*e + C1(x)
где C1(x) и C2(x)
согласно методу вариации постоянных найдём из системы:
::
d d
--(C1(x))*y1(x) + --(C2(x))*y2(x) = 0
dx dx
::
d d d d
--(C1(x))*--(y1(x)) + --(C2(x))*--(y2(x)) = f(x)
dx dx dx dx
где
y1(x) и y2(x) - линейно независимые частные решения ЛОДУ,
y1(x) = 1 (C1=1, C2=0),
y2(x) = exp(2*x) (C1=0, C2=1).
А свободный член f = - s, или
::
/ 2\ x
f(x) = \1 + x /*e
Значит, система примет вид:
::
d 2*x d
--(C2(x))*e + --(C1(x)) = 0
dx dx
::
d d d d / 2*x\ / 2\ x
--(1)*--(C1(x)) + --(C2(x))*--\e / = \1 + x /*e
dx dx dx dx
или
::
d 2*x d
--(C2(x))*e + --(C1(x)) = 0
dx dx
::
d 2*x / 2\ x
2*--(C2(x))*e = \1 + x /*e
dx
Решаем эту систему:
::
/ 2\ x
d -\1 + x /*e
--(C1(x)) = -------------
dx 2
::
/ 2\ -x
d \1 + x /*e
--(C2(x)) = ------------
dx 2
- это простые дифф. ур-ния, решаем их
::
/
|
| / 2\ x
| -\1 + x /*e
C1(x) = C3 + | ------------- dx
| 2
|
/
::
/
|
| / 2\ -x
| \1 + x /*e
C2(x) = C4 + | ------------ dx
| 2
|
/
или
::
/ 2 \ x
\-3 - x + 2*x/*e
C1(x) = C3 + ------------------
2
::
/ 2 \ -x
\-3 - x - 2*x/*e
C2(x) = C4 + -------------------
2
Подставляем найденные C1(x) и C2(x) в
::
2*x
y(x) = C2(x)*e + C1(x)
Получаем окончательный ответ:
::
x 2*x 2 x
y(x) = C3 - 3*e + C4*e - x *e
где C3 и C4 есть константы