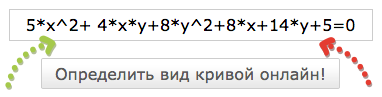
Приведём примеры кривых второго порядка, для которых можно определить канонический вид онлайн:
Кривая
| Уравнение | Канонический вид | Тип | Измерение |
|---|---|---|---|
| 9x^2+12xy+4y^2-24x-16y+3=0 | x^2=1 | Две параллельные прямые | Кривая |
| x^2-2xy+y^2-10x-6y+25=0 | y^2=4*sqrt(2)*x | Парабола | Линия |
| 5x^2+4xy+y^2-6x-2y+2=0 | x^2/(1/sqrt(2*sqrt(2)+3))^2 + y^2/(1/sqrt(-2*sqrt(2)+3))^2=0 | Вырожденный эллипс | Линия |
| 5*x^2+ 4*x*y+8*y^2+8*x+14*y+5=0 | x^2/(3/4)^2+y^2/(1/2)^2=1 | Эллипс |
Ислледование на определение вида кривой будет выглядеть примерно так:
Имеется два способа: Прямой метод и метод инвариантов:
Дано ур-ние кривой 2-порядка: $$5 x^{2} + 4 x y + 8 x + 8 y^{2} + 14 y + 5 = 0$$ Это уравнение имеет вид: $$a_{11} x^{2} + 2 a_{12} x y + 2 a_{13} x + a_{22} y^{2} + 2 a_{23} y + a_{33} = 0$$ где $$a_{11} = 5$$ $$a_{12} = 2$$ $$a_{13} = 4$$ $$a_{22} = 8$$ $$a_{23} = 7$$ $$a_{33} = 5$$ Вычислим определитель $$\Delta = \left|\begin{matrix}a_{11} & a_{12}\\a_{12} & a_{22}\end{matrix}\right|$$ или, подставляем $$\Delta = \left|\begin{matrix}5 & 2\\2 & 8\end{matrix}\right|$$ $$\Delta = 36$$ Т.к. $$\Delta$$ не равен 0, то находим центр канонической системы координат. Для решаем систему уравнений $$a_{11} x_{0} + a_{12} y_{0} + a_{13} = 0$$ $$a_{12} x_{0} + a_{22} y_{0} + a_{23} = 0$$ подставляем коэффициенты $$5 x_{0} + 2 y_{0} + 4 = 0$$ $$2 x_{0} + 8 y_{0} + 7 = 0$$ тогда $$x_{0} = - \frac{1}{2}$$ $$y_{0} = - \frac{3}{4}$$ Тем самым мы перешли к уравнению в системе координат O'x'y' $$a'_{33} + a_{11} x'^{2} + 2 a_{12} x' y' + a_{22} y'^{2} = 0$$ где $$a'_{33} = a_{13} x_{0} + a_{23} y_{0} + a_{33}$$ или $$a'_{33} = 4 x_{0} + 7 y_{0} + 5$$ $$a'_{33} = - \frac{9}{4}$$ тогда ур-ние превратится в $$5 x'^{2} + 4 x' y' + 8 y'^{2} - \frac{9}{4} = 0$$ Делаем поворот системы полученной координат на угол φ $$x' = \tilde x \cos{\left (\phi \right )} - \tilde y \sin{\left (\phi \right )}$$ $$y' = \tilde x \sin{\left (\phi \right )} + \tilde y \cos{\left (\phi \right )}$$ φ - определяется из формулы $$\cot{\left (2 \phi \right )} = \frac{a_{11} - a_{22}}{2 a_{12}}$$ подставляем коэффициенты $$\cot{\left (2 \phi \right )} = - \frac{3}{4}$$ тогда $$\phi = - \frac{1}{2} \operatorname{acot}{\left (\frac{3}{4} \right )}$$ $$\sin{\left (2 \phi \right )} = - \frac{4}{5}$$ $$\cos{\left (2 \phi \right )} = \frac{3}{5}$$ $$\cos{\left (\phi \right )} = \sqrt{\frac{1}{2} \cos{\left (2 \phi \right )} + \frac{1}{2}}$$ $$\sin{\left (\phi \right )} = \sqrt{- \cos^{2}{\left (\phi \right )} + 1}$$ $$\cos{\left (\phi \right )} = \frac{2 \sqrt{5}}{5}$$ $$\sin{\left (\phi \right )} = - \frac{\sqrt{5}}{5}$$ подставляем коэффициенты $$x' = \frac{2 \sqrt{5}}{5} \tilde x + \frac{\tilde y}{5} \sqrt{5}$$ $$y' = - \frac{\tilde x}{5} \sqrt{5} + \frac{2 \sqrt{5}}{5} \tilde y$$ тогда ур-ние превратится из $$5 x'^{2} + 4 x' y' + 8 y'^{2} - \frac{9}{4} = 0$$ в $$8 \left(- \frac{\tilde x}{5} \sqrt{5} + \frac{2 \sqrt{5}}{5} \tilde y\right)^{2} + 4 \left(- \frac{\tilde x}{5} \sqrt{5} + \frac{2 \sqrt{5}}{5} \tilde y\right) \left(\frac{2 \sqrt{5}}{5} \tilde x + \frac{\tilde y}{5} \sqrt{5}\right) + 5 \left(\frac{2 \sqrt{5}}{5} \tilde x + \frac{\tilde y}{5} \sqrt{5}\right)^{2} - \frac{9}{4} = 0$$ упрощаем $$4 \tilde x^{2} + 9 \tilde y^{2} - \frac{9}{4} = 0$$ Данное уравнение является эллипсом $$\frac{\tilde x^{2}}{\left(\frac{3}{4}\right)^{2}} + \frac{\tilde y^{2}}{\left(\frac{1}{2}\right)^{2}} = 1$$ - приведено к каноническому виду.
Центр канонической системы координат в точке O:
(-1/2, -3/4)
Базис канонической системы координат $$\vec e_1 = \left ( \frac{2 \sqrt{5}}{5}, \quad - \frac{\sqrt{5}}{5}\right )$$ $$\vec e_2 = \left ( \frac{\sqrt{5}}{5}, \quad \frac{2 \sqrt{5}}{5}\right )$$
Метод инвариантов
Дано ур-ние линии 2-порядка: $$5 x^{2} + 4 x y + 8 x + 8 y^{2} + 14 y + 5 = 0$$ Это уравнение имеет вид: $$a_{11} x^{2} + 2 a_{12} x y + 2 a_{13} x + a_{22} y^{2} + 2 a_{23} y + a_{33} = 0$$ где $$a_{11} = 5$$ $$a_{12} = 2$$ $$a_{13} = 4$$ $$a_{22} = 8$$ $$a_{23} = 7$$ $$a_{33} = 5$$ Инвариантами данного уравнения при преобразовании координат являются определители: $$I_{1} = a_{11} + a_{22}$$
|a11 a12|
I2 = | |
|a12 a22|
$$I_{3} = \left|\begin{matrix}a_{11} & a_{12} & a_{13}\\a_{12} & a_{22} & a_{23}\\a_{13} & a_{23} & a_{33}\end{matrix}\right|$$ $$I{\left (\lambda \right )} = \left|\begin{matrix}a_{11} - \lambda & a_{12}\\a_{12} & a_{22} - \lambda\end{matrix}\right|$$
|a11 a13| |a22 a23|
K2 = | | + | |
|a13 a33| |a23 a33|
подставляем коэффициенты $$I_{1} = 13$$
|5 2|
I2 = | |
|2 8|
$$I_{3} = \left|\begin{matrix}5 & 2 & 4\\2 & 8 & 7\\4 & 7 & 5\end{matrix}\right|$$ $$I{\left (\lambda \right )} = \left|\begin{matrix}- \lambda + 5 & 2\\2 & - \lambda + 8\end{matrix}\right|$$
|5 4| |8 7|
K2 = | | + | |
|4 5| |7 5|
$$I_{1} = 13$$ $$I_{2} = 36$$ $$I_{3} = -81$$ $$I{\left (\lambda \right )} = \lambda^{2} - 13 \lambda + 36$$ $$K_{2} = 0$$ Т.к. $$I_{2} > 0 \wedge I_{1} I_{3} < 0$$ то по признаку типов линий:
данное уравнение имеет тип : эллипс.
Составляем характеристическое уравнение для нашей линии: $$- I_{1} \lambda + I_{2} + \lambda^{2} = 0$$ или $$\lambda^{2} - 13 \lambda + 36 = 0$$ $$\lambda_{1} = 9$$ $$\lambda_{2} = 4$$ тогда канонический вид уравнения будет $$\tilde x^{2} \lambda_{1} + \tilde y^{2} \lambda_{2} + \frac{I_{3}}{I_{2}} = 0$$ или $$9 \tilde x^{2} + 4 \tilde y^{2} - \frac{9}{4} = 0$$ $$\frac{\tilde x^{2}}{\left(\frac{1}{2}\right)^{2}} + \frac{\tilde y^{2}}{\left(\frac{3}{4}\right)^{2}} = 1$$ - приведено к каноническому виду.